Heat diffusion during thin-film composite membrane formation

Schematic illustration of heat transfer in during interfacial polymerization for the fabrication of thin-film composite membrane selective layers
Thin-film composite (TFC) membranes, the backbone of modern reverse osmosis and nanofiltration, combine the high separation performance of a thin selective layer with the robust mechanical support. Previous studies have shown that heat released during interfacial polymerization (IP) can have a significant impact on the physical and chemical structure of the selective layer. In this study, we develop a multilayer transient heat conduction model to analyze how the thermal properties of the materials used in TFC fabrication impact interfacial temperature, focusing on support-free (SFIP), conventional (CIP), and interlayer-modulated IP (IMIP). Using a combination of analytic solutions and computational models, we demonstrate that the thermal effusivities of fluid and material layers can have a significant effect on the temporal evolution of interfacial temperature during IP. In CIP, we show that the presence of a polymeric support adjacent to the reaction interface yields a 20% to 60% increase in interfacial temperature rise, lasting for ∼ 0.1 s. Furthermore, we demonstrate that inorganic or metallic interlayers, which have high thermal effusivities, can lead to short-lived order-of-magnitude reductions in interfacial temperature rise. Finally, we provide analytical approximations for transient heat conduction through multilayered systems, enabling rapid evaluation of the thermal impact of novel membrane support and interlayer materials and structures on interfacial temperature during TFC fabrication. Quantifying how the thermal properties of solvents, support layers, and interlayers affect interfacial temperature during IP is critical for the rational design of new TFC membranes.
A. Deshmukh, J.H. Lienhard, and M. Elimelech, “Heat Diffusion During Thin-Film Composite Membrane Formation,” J. Membrane Science, 696:122493, March 2024.
Heat transfer in flat-plate boundary layers: a correlation for laminar, transitional, and turbulent flow
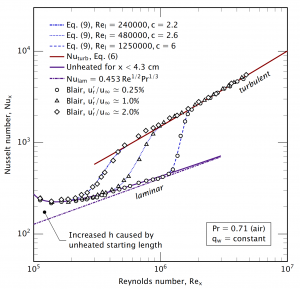
Proposed correlation, Eq. (9), compared to constant heat flux data of Blair for three levels of free stream turbulence.
J.H. Lienhard V, “Heat transfer in flat-plate boundary layers: a correlation for laminar, transitional, and turbulent flow,” J. Heat Transfer, online 31 March 2020, 142(6):061805, June 2020. (doi: Open access) (presentation) (one-page summary) (DSpace)
Accurate linearization of non-gray radiation heat exchange
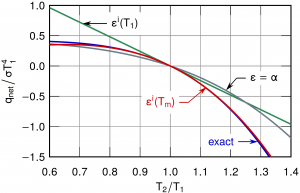
The internal emissivity based on mean temperature is in good agreement with the exact heat exchange for even extremely non-gray surfaces.
J.H. Lienhard V, “Linearization of Non-gray Radiation Exchange: The Internal Fractional Function Reconsidered,” J. Heat Transfer, online 3 Dec. 2018, 141(5):052701, May 2019. (OPEN ACCESS) (preprint) (presentation)